标题：Beyond pairwise mechanisms of species coexistence in complex communities

日期：2017年6月1日

作者：Jonathan M. Levine

单位：苏黎世联邦理工学院，整合生物研究所环境系统科学系

摘要

生态群落中物种的巨大多样性促使人们对维持生物多样性的机制进行了一个世纪的研究。然而，这方面的大部分工作考察的是公平竞争对的共存。这种方法忽略了只有在多样化竞争网络中才会出现的共存机制。尽管这些机制有可能创造条件，使一个竞争者的丧失引发其他竞争者的丧失，但我们缺乏必要的知识来判断它们对自然界共存的重要性。进步需要从多营养相互作用网络的研究中借鉴洞察力，并将经验数据与竞争模型相结合。

正文

关于物种共存的生态学研究的目的是解释尽管物种之间的竞争能力存在差异，但我们在自然界中看到的物种的巨大多样性是如何持续存在的。然而，从经验上评估大量竞争者之间的相互作用在逻辑上是具有挑战性的，而且许多用于分析一对竞争者之间相互作用的数学工具并不容易转化为竞争物种的大型网络。因此，共存研究主要集中在竞争对手之间的机制上。尽管强调两两共存可能被证明是有效的，并且通过两两方法在理解物种多样性的维持方面取得了很大进展（Box 1），生态学家很难证明不同生态系统中许多物种的共存是两两机制的结果。在亚马逊雨林25公顷的土地上发现的1000多种热带树种共存的可能性有多大，因为竞争对手之间存在无数的成对生态位差异？

对于物种丰富的群落的共存，一个诱人的解释涉及到只有在不同的竞争系统中才会出现的机制。事实上，超过两个竞争者的系统形成了一个竞争关系网络，其结构应该影响整个系统的动态。在多大程度上，研究孤立的物种对之间的共存能够帮助我们理解复杂竞争网络的动态，这一点尚不清楚。然而，众所周知，网络结构可以强烈地决定互惠和多营养网络对扰动的鲁棒性，并从根本上改变成对相互作用的结果。因此，我们可以预期，网络结构对不同竞争系统的动态也会产生类似的强大影响。

为了更好地理解物种多样性的维持，生态学家必须更好地探索多样性竞争网络结构所导致的共存机制。我们进一步建议，通过将互惠和多营养网络研究的经验教训应用于竞争系统，可以加速这种理解。重要的是，更好地理解只在不同系统中出现的共存机制将有助于阐明生物多样性的稳定性。根据定义，随着物种的消失，这些共存机制受到侵蚀。因此，一个竞争者的丧失可能导致其他竞争者的随之丧失，这是一个从营养和互助网络的理论研究中众所周知的灭绝级联，但很少在竞争系统中进行研究。

在这里，我们讨论了共存机制的理论和实证文献，这些机制只出现在两个以上竞争对手的网络中。尽管这些机制在近50年前就用数学模型证明了，但对其运作的令人信服的经验测试仍然很少，这使得这些相互作用对自然界共存的影响仍然未知。虽然我们只关注竞争对手之间的相互作用，但在整个综述中，我们强调了营养和互惠网络研究的发现，这些发现有助于展示不同竞争网络的运作方式和分析方式。然后，我们制定了一个路线图，以促进对共存机制的理解，这种机制只出现在两个以上物种的系统中。这包括对这些机制何时可能起作用形成一种预测性的理解，从经验上评估它们在自然界中的普遍性和重要性，并从理论上证明它们如何影响真正多样化系统中的共存。

两个以上竞争者共存

理论表明，两种竞争动态-相互作用链和高阶相互作用（只出现在三个或更多物种的网络中）（图1）。这种相互作用不一定稳定，实际上可能破坏共存。因此，我们首先定义了这些相互作用，然后解释了它们促进物种丰富度的条件-我们在本综述中衡量多样性的标准。

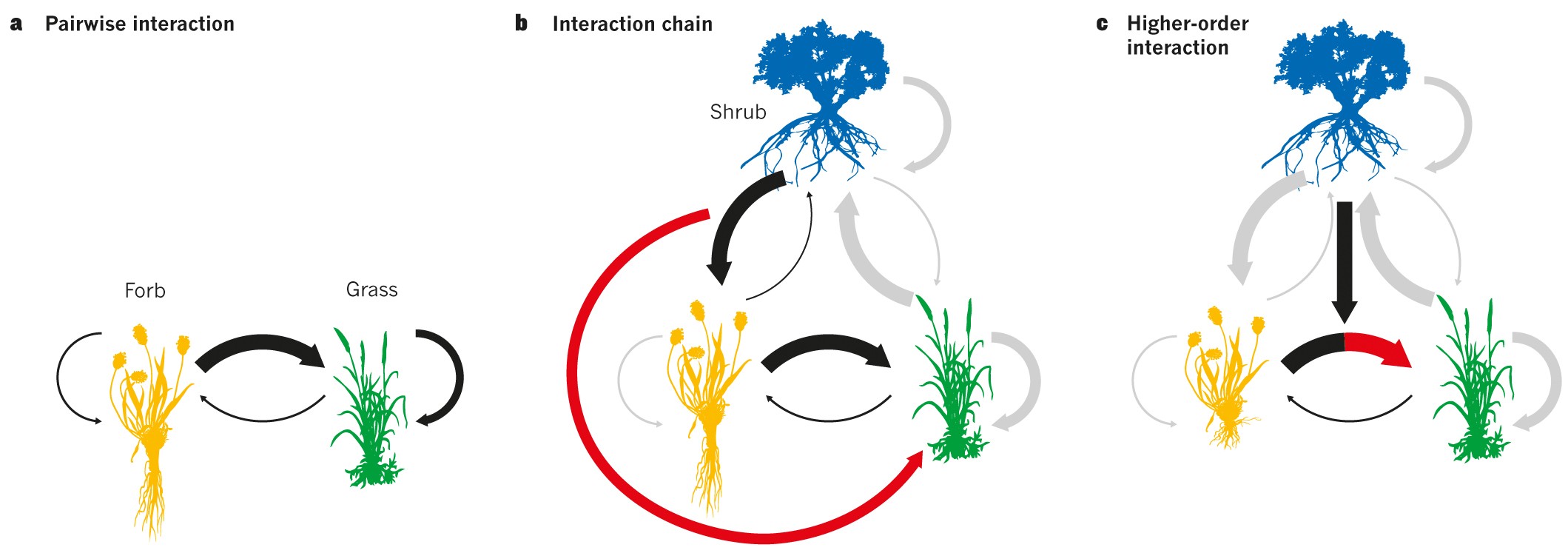
图1 只有两个以上的竞争者才会出现共存机制

a，一种牧草和一种草之间严格的两两竞争，显示种间和种内的相互作用；

b，灌木通过抑制牧草提供间接利益（红箭头）的相互作用链。灰色箭头表示不直接涉及交互链或高阶交互的成对交互；

c，灌木改变牧草对草的人均影响的高阶相互作用。在这种情况下，灌木引起杂草变化，导致它在土壤的较浅深度扎根，使它与草有更大的竞争接触。

a-c中的箭头宽度表示人均竞争效应的强度。

当两两竞争的相互作用嵌入到其他（仍然是两两）相互作用的网络中时，相互作用链就出现了。正如在营养级联中一样，间接效应是由与焦点对中两个物种相互作用的第三种（或更多）物种的密度变化引起的（图1b）。即使所有直接的成对相互作用都是消极的，这些间接影响往往是积极的。研究得最好的稳定竞争网络包括三个物种之间的非传递性竞争，就像石头-剪刀布-布游戏的基础。虽然物种之间的相互作用基本上仍然是成对的，但稳定的动力学是通过将这些成对的相互作用串在一起而产生的，因此密度的变化通过网络传播，形成一个抵消初始扰动的负反馈回路。

当物种之间的相互作用不再是基本成对时，高阶相互作用就出现了。相反，一个竞争者对另一个竞争者的人均影响取决于第三、第四或第五种(或可能更多)物种的种群密度（图1c）。这些相互作用类似于营养文献中描述的性状介导的间接相互作用，其中高阶相互作用发生在捕食者，例如，通过对更低营养水平的级联效应来改变猎物的行为。竞争对手之间的高阶相互作用不如相互作用链那么直观，但当一个物种对另一个物种具有可塑性形态或行为反应时，就会出现高阶相互作用，例如图1c所示的杂草扎根深度的减少，这改变了杂草与第三种物种的竞争。在一个较少假设的例子中，车前草（Plantago lanceolata）抑制红羊茅（Festuca rubra）的根系生长，而红羊茅是土壤养分的有效竞争对手。这种可塑性反应反过来又会削弱红羊茅对其他营养有限的竞争对手生产性能的人均影响。更一般地说，当一个物种的存在削弱了另两个物种的种间相互作用时，高阶相互作用可能会稳定共存。

相互作用链和高阶相互作用之间的区别取决于间接效应是来自竞争者密度（相互作用链）的变化还是来自人均竞争效应（高阶相互作用）的变化。因此，相互作用链和高阶相互作用在其操作的时间尺度上有所不同。在高阶互动中，一个竞争者会立即改变另外两个竞争者之间的竞争（例如，通过改变个体特征）。相比之下，在相互作用链中，竞争对手通过改变其他竞争对手的密度来改变另两个物种之间的相互作用，因此应该在更大的时间滞后后出现。尽管相互作用链和高阶相互作用的定义不同，但它们都需要多样性来运作，因此两者都可能使系统容易受到灭绝级联的影响。这种动态最简单的例子是，一个竞争对手从一个由不可传递竞争循环稳定的系统中流失，这将导致其他竞争对手的流失（图2）。

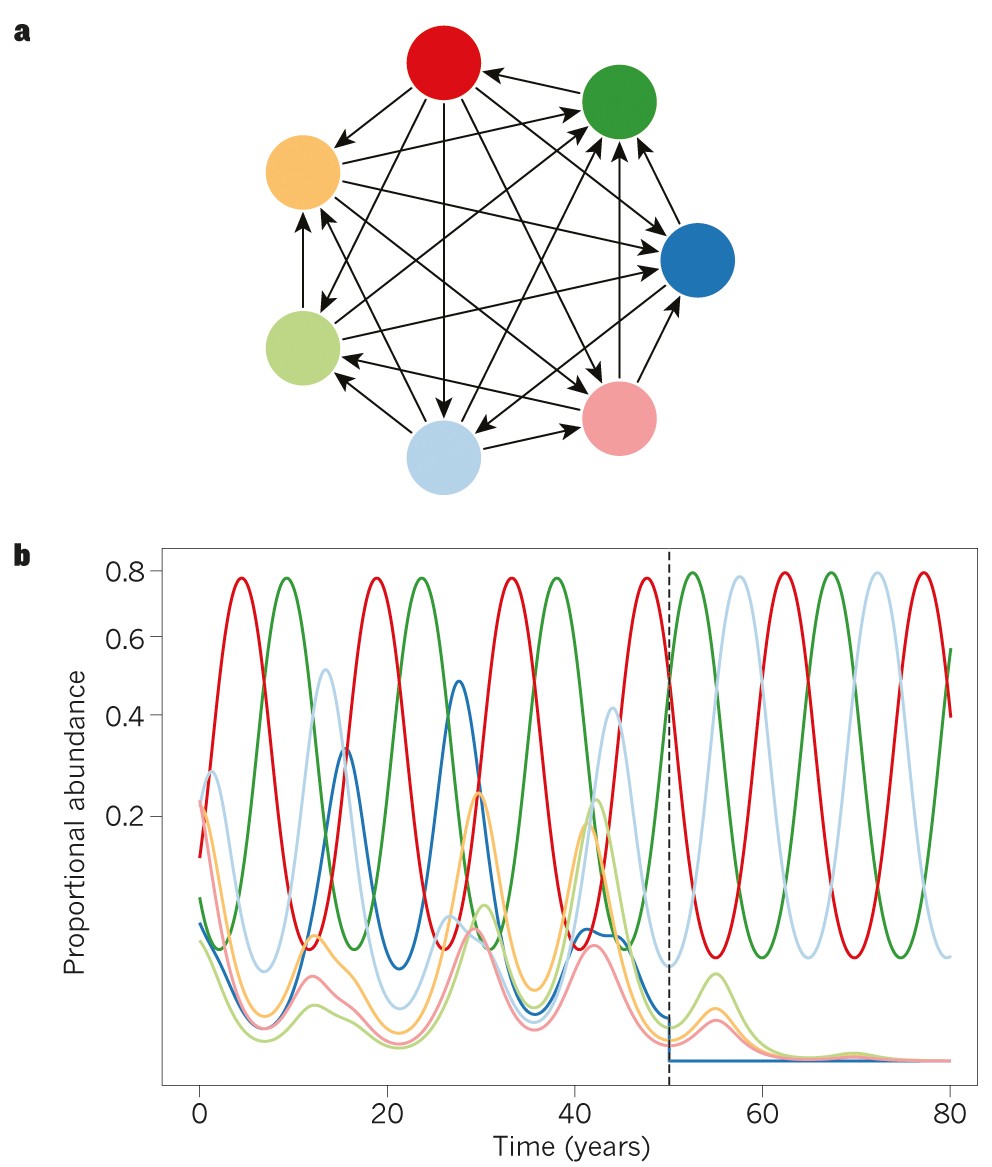
图2 竞争网络和消失级联

a，一种不可传递的竞争网络或“锦标赛”，其中箭头在成对竞争中指向胜利者和失败者。该系统由许多较小的不可传递循环（例如，在浅蓝色，深蓝色和粉红色物种之间）组成，这些循环嵌套在包含所有七个物种的较大循环中；

b、按照参考文献6的方法对系统进行动力学仿真。由于intransitive竞争关系，图中所示的7个物种将无限期共存，在一个平衡中循环，其中红色和深绿色物种的比例丰度（属于每个物种的个体比例）为1/3，浅蓝色和深蓝色物种的比例丰度为1/9，浅绿色、橙色和粉红色物种的比例丰度为1/27。在50年，深蓝色物种被送去灭绝，这导致另外3个物种由于稳定其动态的非及物性被破坏而灭绝。剩下的三个物种以石头剪刀布的方式在1/3的比例丰度上下波动。y轴以平方根尺度表示，以提高低丰度物种表示。

对交互链的理论见解

理论生态学家早就意识到，当物种嵌入到一个多样化的竞争网络中时，成对竞争相互作用的结果会发生变化。这种理解的大部分最初是受到Lotka-Volterra系统研究的启发，该系统描述了不同物种之间的相互作用，通常模拟了整个群落对平衡周围的小扰动的反应（Box 2）。随后的工作表明，当从分布中随机抽样种间竞争相互作用强度时，更多样化的群落不太可能稳定。虽然这一发现表明，共存的机会随着物种数量的增加而减少，但这在一定程度上是随机网络结构的函数——不可传递的竞争结构可以改变这种期望。

一个平行的研究课程探讨了特定的竞争关系（网络结构），这种关系使得两个物种之间的竞争结果能够通过包含额外的竞争者而改变。第三个竞争者的加入可以产生平衡或稳定的效果，从而有利于共存（如Box 1）。例如，一个较强的竞争者可以通过区别地损害两个竞争者中的较强者来促进另外两个竞争者的共存。在这种相互作用结构下，优势种平衡了其他两个竞争对手的平均适应度，但没有通过引入新的共存机制来稳定它们的动态。任何长期共存仍然需要如Box 1所定义的成对生态位差异。相反，当三个物种形成非传递竞争循环时，这种结构可以稳定共存。

当物种不能按简单的线性竞争等级进行排序时，就会发生非传递性竞争。这种机制是稳定的，因为减少任何竞争对手在循环中的丰度通过网络传播，以一种反馈的方式有利于受干扰物种的恢复。然而，这些稳定的动力学只出现在物种数量为奇数的系统中;当存在偶数个竞争者时，这种机制不能产生共存，这就提出了关于这些系统如何组合的有趣问题。这种相互作用的最基本模型在有向图中对物种之间的竞争优势进行编码，其中节点代表物种，对于每对，一个称为“边”的箭头将竞争赢家与输家连接起来（图2a）。在最简单的非及物竞争中，三个物种形成一个石头剪刀布的非及物循环，这已经证明了三个竞争者可能共存，尽管有循环。包含许多物种的更大的网络已经通过模拟或编写确定性方程进行了探索，例如进化博弈论的核心复制因子方程（图2b）。

在应用于相互作用链的其他建模方法中，竞争较少不对称，但三个竞争者之间的不可及性仍然强有力地稳定了动态。例如，May和Leonard研究了三个物种（这里称为A、B和C）的Lotka-Volterra模型，其中竞争系数的选择使得A受B的影响比B受A的影响大，B受C的影响比C受B的影响大，C受A的影响比A受C的影响大。因此，所有系数都是负的，但那些幅度最大的系数被安排在石头剪刀布的循环中。这样的模型可以产生所有三个物种的鲁棒极限环，而不是在传递竞争下预期的垄断。类似的机制促进了具有明确的消费者-资源相互作用、连续替代或竞争、殖民化和空间抢占之间权衡的模式的共存。

虽然非及物竞争对共存的具体影响突出了将成对竞争相互作用嵌入多样化竞争对手网络的重要性，但网络结构如何更普遍地影响多样化竞争社区的动态却很少被明确探讨。然而，对网络结构重要性的含蓄承认来自理论生态学家的共同实践，即根据产生特定互动结构的规则建立竞争对手社区。例如，模型通常假定一个物种对另一个物种的人均影响是它们在沿着共同生态位轴利用资源时重叠的函数。此外，众所周知，在其他类型的相互作用网络中，网络结构会强烈影响物种的持久性。例如，食物网往往是按隔间组织的，其中一个隔间内的物种彼此之间的互动比它们与其他隔间的物种之间的互动更频繁。有趣的是，这种区块结构可以缓冲扰动在整个网络中的传播，并且可以在由不可传递的竞争关系稳定的网络中发挥类似的作用。互惠相互作用的网络，例如开花植物和它们的传粉者或种子传播者之间形成的网络，往往以嵌套的方式组织起来，这意味着专门的动物与植物物种的适当子集相互作用，这些子集也与更通用的动物相互作用。这种嵌套的网络结构可以增加共生网络中共存物种的数量。

在为数不多的明确询问网络结构如何影响竞争对手动态的当代研究中，Barabas等人3探讨了相互作用矩阵（Box 2）中系数的安排如何影响不同竞争系统的稳定性和可行性。他们发现，通过以嵌套的方式排列相互作用系数，并将它们排列成块，可以实现最大和最小的稳定性。这项工作表明，宏观网络属性，如分隔和嵌套性，可能对竞争社区有重要影响，正如其他交互类型所知的那样。

不及物竞争的经验证据

竞争对手之间的互动链会对竞争网络的动态产生一系列的影响，尽管对稳定共存起特殊作用的互动链——不可传递的竞争循环——在这里特别相关。直接的经验证据表明，不及物竞争在自然界中普遍存在，研究报告强烈支持及物性或普遍不及物性存在潜在问题。非传递性相互作用的两个最令人信服的例子实际上涉及物种内部的竞争，而不是物种之间的竞争。Kerr等人表明，大肠杆菌工程菌株之间存在非传递性相互作用，而Sinervo和Lively则表明，这些相互作用存在于蜥蜴种群中具有不同交配策略的个体之间。Lankau和Strauss提供的数据连接了“种内”和“种间”的非传递性证据，他们表明，非传递性竞争发生在两个选择性繁殖的黑芥菜(Brassica nigra)种群和第三个异种的植物竞争对手之间。然而，作者的数学模型表明，自然选择应该驱使芥菜种群采取单一的最优策略，使系统崩溃，使物种之间两两共存。非传递竞争的最佳物种水平证据来自海洋无根生物的群体过度生长模式。然而，即使在这些系统中，观察到的物种三胞胎之间的非传递性竞争也嵌入在一个更大的主要传递相互作用的矩阵中。

评估不及物性普遍程度的另一种方法是分析实验结果，在这些实验中，许多物种(通常是温室环境中的植物)在成对试验中相互竞争。虽然这些研究通常得出的结论是，非传递性是罕见的，但它们通常通过相对产量或相关措施来衡量竞争优势，其中单株植物与异种邻居或邻居的生长是通过其与本物种邻居的生长来衡量的。这种方法衡量不同物种对共同目标单株植物的人均竞争效应的差异（见补充说明）。然而，机制和现象学模型都表明，竞争优势不是来自物种的人均竞争效应的差异，而是来自物种容忍种内和种间竞争对手影响的能力差异。相对产量不能深入了解物种如何忍受竞争，因此不能揭示竞争结果(补充说明)。

另一种方法是从野外样地的物种丰度模式推断成对竞争优势网络。该方法的应用表明，植物群落中普遍存在着不可及性，不可及性的程度与物种丰富度之间存在着正相关关系。然而，该方法是建立在低空间环境异质性和物种替代密度无关概率的假设基础上的，因此推断的竞争矩阵不考虑生态位的配对差异（Box 1）。尽管该方法可能适用于在没有其他物种丰度控制的假设下，询问哪种非传递性网络结构与丰度模式最一致，它并不适合于评价非及物性是否比两两机制更简洁地解释丰度模式或共存。

总的来说，现有的关于非传递性竞争的实证文献包括几个物种内部（而不是物种之间）的非传递性循环的很好解决的例子，对竞争优势的不正确估计的实验分析，以及建立在缺乏成对生态位差异的前提下的逆模型。这些方法提供的证据使得很难解决自然界中不可及性竞争的真正普遍性。然而，普遍性只是问题的一部分，因为更明显的是缺乏证据来评估观察到的不可及性在多大程度上稳定了自然界的共存。

对高阶相互作用的理论见解

物种之间的相互作用基本上是成对的，这一假设几乎是所有共存理论的核心。然而，从经验的角度来看，我们几乎不知道这种假设是否正确。物种相互作用实际上可能是由两个以上竞争者之间的多向关系（三向、四向甚至更高阶的相互作用）引起的。Abrams表明，在资源竞争的经典模型中，高阶相互作用经常出现在非物流资源增长或消费者对资源密度的非线性函数响应中。这一结果提出了一个重要的观点，即高阶相互作用与成对竞争的根本不同，这在一定程度上是研究物种共存的现象学方法的产物。这种方法使用相互作用系数来描述一个竞争者对另一个竞争者的负面影响，而不是使用与共享资源或消费者的明确相互作用，这在更机械的竞争模型中发生。在机械模型中，不需要添加特殊的高阶项，高阶相互作用就可以从潜在的生物学中有机地出现。然而，无论考虑竞争的现象学模型还是机制模型，任何两个物种之间的相互作用在多大程度上是由系统中其他物种决定的，仍然是一个相关的问题。

另一种理论显示了如何利用网络框架来研究高阶相互作用。与用箭头连接物种（节点）的图不同，在两两相互作用的网络中，高阶相互作用用超图表示，其中箭头将节点连接到其他箭头（如图1c）。正如竞争系数的n × n矩阵（n =物种数量）用于参数化假设成对相互作用的方程组一样，n × n × n张量（多维数组）可用于描述三方相互作用，其中每个元素描述两种物种对第三种相互作用的联合效应。尽管这样一个张量描述了所有可能发生作用的高阶相互作用，但由于个体生物的有限性和无根生物只与邻近生物相互作用的事实，这些相互作用在自然界中的实际作用是复杂的。同时，高阶相互作用（和相互作用链）的稳定效应可以潜在地补偿人口统计学随机性对物种丰富度的抑制效应。

尽管普遍认为高阶相互作用应该在生态系统中普遍存在，但它们通常被排除在竞争模型之外。因此，生态学家对这种相互作用应该如何影响竞争结果缺乏明确的预期。此外，由于缺乏关于这些相互作用是如何构成的经验证据，理论几乎没有立足的基础。因此，一个合理的出发点是考虑随机高阶相互作用的影响——正如Bairey等人的模型所包含的那样。作者表明，包括越来越高阶和随机分配值的相互作用，逆转了May的经典结果，即群落多样性破坏了生态系统的稳定。在严格的四向相互作用下，更多样化的群落可以更好地承受更强的相互作用带来的不稳定影响，因此，一个物种的消失会使剩下的系统更容易灭绝。Bairey研究了由竞争者、消费者和互惠者组成的社区的稳定性，尽管类似的结果可能适用于纯粹的竞争系统。然而，Bairey等人的研究不应被解释为表明高阶相互作用必然是稳定的。与相互作用链一样，高阶相互作用的结果应该取决于网络的结构和高阶效应的标志——这些主题尚未得到相当多的实证关注。

高阶相互作用的经验证据

虽然不同营养水平的物种之间的高阶相互作用是相当多研究的主题，但竞争对手之间的这种相互作用却鲜为人知。评估三个物种之间高阶相互作用运作的经典方法——以及大多数现有工作的范围——包括评估物种在所有双向和三向组合中的表现。处理的数量通常限制了这些实验的可处理的实验室模型系统，如果蝇，原生生物和池塘微甲壳类动物。使用这种设计，通常通过方差分析（ANOVA），可以测试焦点物种对孤立的其他物种（成对竞争）的反应如何预测焦点物种对多个竞争对手(三胞胎组合)的反应。然而，方差分析检验也可以在两个竞争者对焦点物种的影响之间产生显著的统计相互作用，因此表明存在高阶相互作用，即使每个竞争者对焦点物种的影响是独立的。此外，在竞争对手密度变化的时间框架内进行的实验中，很难证明明显的高阶相互作用不是由竞争对手丰度的变化引起的，这将使其成为“误诊”的相互作用链。由于这个原因，以及实验发生的实验室环境，这些实验通常没有提供高阶相互作用是否普遍存在于自然界生态群落的明确测试。

一种相关的方法包括将种群动态或生物量积累模型拟合到竞争实验中，并评估纯成对相互作用的模型如何能够预测个体的表现或多物种系统的动态。用这种方法量化高阶相互作用是一项艰巨的经验和统计挑战。虽然描述n个物种之间的所有成对相互作用需要n2个系数的经验估计，但估计所有三重态相互作用需要多达n3个系数。为了简化设计，Weigelt在实验阵列中种植单一物种的焦点植物，周围是同种个体，或来自一个、两个或三个其他物种的个体。然后，他们建立了一系列模型来描述焦点植物的生物量是如何被邻居减少的。在测试的三个或更多的竞争对手组合中，有三分之一的模型具有成对效应和相互作用项，可以最好地描述个体生物量随邻居密度的下降，这表明存在高阶相互作用。Mayfield和Stouffer开发了更高阶相互作用的更直接的统计测试，然后将他们的方法应用于澳大利亚西南部一年生植物群落收集的观测数据。他们发现，高阶相互作用显著影响了六种焦点物种中的三种的繁殖力，往往削弱了邻居的抑制作用。

除了量化高阶相互作用的技术挑战外，一个核心问题是很少有实证研究真正评估这些相互作用的生态重要性。事实上，有人提出，因为高阶相互作用几乎肯定在自然界中起作用，而证明它们只需要有足够的自由度，真正的问题是，在其他生态不确定性来源的背景下，高阶相互作用是否会产生明显的后果68。不幸的是，很难评估这种相互作用如何影响共存，因为很少有研究测量可以通过竞争性种群动态模型转化为动态的响应变量。生态学家可能有更好的证据来评估高阶相互作用，而不是相互作用链，但证据仍然很少，而且很难通过目前的工作来评估这些相互作用如何调节自然界中的群落动态。

n个物种的研究

促进我们对共存机制的理解，这种共存机制只在两个以上竞争者的系统中运作，需要获得三种类型的知识。首先，我们需要建立更好的预期，即非传递性竞争关系和稳定的高阶互动何时以及如何在竞争社区中出现。其次，我们需要获得关于自然界中这些相互作用的普遍性和重要性的明确的经验证据。最后，我们需要为这些机制如何影响真正多样化社区的共存提供理论指导。在这里，我们列出了一个研究过程，应该解决这些主要的悬而未决的问题。

何时期待复杂的共存机制

很多关于互动链和高阶互动的研究都涉及到竞争的现象学模型。对于理论家来说，这些模型能够有效地评估共存相互作用的后果，而对于经验主义者来说，这些模型提供了有限数量的参数来拟合数据。然而，在现象学模型中插入高阶术语或非传递性竞争循环并不有助于建立对自然中非传递性竞争和高阶相互作用何时出现的预测性理解。发展这样一种理解是很重要的，因为这些机制的量化是具有挑战性的，而且只有当我们有理由认为它们起着强有力的作用时，我们才会想要进行这项工作。此外，高阶相互作用需要消除神秘感，成为生态学家设想共存的常规部分，确定其机制基础是实现这一目标的一种方式。作为问题严重程度的一个例子，即使是提出高阶相互作用存在的实证研究也很少为观察到的相互作用提供机制。因此，我们提倡探索明确包含资源或捕食者动态的不同网络中竞争相互作用的机制模型。

Huisman和Weissing已经证明了理解不及物竞争关系的更机械方法的价值。他们建立了消费者-资源模型，并展示了在由三个物种组成的系统中出现传递竞争和非传递竞争的条件。多重限制资源是通过成对生态位差异共存的重要条件，也是不可传递循环出现的必要条件。在只有一个限制资源的情况下，物种的排名仅仅取决于它们抑制资源的能力，这产生了纯粹的传递竞争关系。类似的方法可以应用于理解出现高阶相互作用所必需的条件，以及这些相互作用是否有利于或损害共存。实现这一目标的初步进展可以通过修改现有的资源竞争模型来实现，例如Tilman的R模型。这将使生态学家能够探索在一个有两个以上竞争对手的系统中何时出现高阶相互作用，如果它们确实出现，这种相互作用如何影响共存和灭绝级联。这些模型中关于特质可塑性的假设可能被证明是重要的;因此，现有的生态进化模型可能是一个有用的起点，其中特征值对竞争相互作用作出反应并产生影响。

在具有多样化竞争对手的模型中添加资源或更高的营养水平既提高了网络的复杂性，又加深了相关的定量挑战。幸运的是，现有的技术可以通过纠正竞争系数来简化多营养系统的结构，使其包括“内部”和“之间”的营养水平相互作用。Bastolla等人开发了这样一个框架，可以计算竞争系统中共存物种数量的上限。这一框架后来被扩展到涉及竞争和互惠互动的物种系统，互惠互动的结构被发现通过调节促进和竞争的相对效应来影响物种共存。根据平均适应度差异和稳定生态位差异（定义见Box 1），也存在重构网络结构影响的方法，这些指标通常用于理解两两共存。例如，Jabot和Bascompte展示了高营养水平相互作用的稳定效应和驱动适应度差异的相互作用之间的平衡是如何通过多营养相互作用网络的结构来调节的。

获得经验证据

普遍缺乏证据来评估相互作用链和高阶相互作用在自然界中的普遍性和重要性，这可能是我们在物种共存研究中最大的知识缺口之一。填补这一空白将需要两项同等重要的努力:量化这种机制在自然群落中的运作;并评估它们对物种共存的重要性。我们认为，在这两个方面向前发展都需要多物种种群模型与观测或实验数据相适应。我们承认，基于模型的方法对于实验室微生物种群可能不是必要的，因为实验室微生物种群更容易提供在成对和更复杂的竞争试验中比较长期竞争结果的选择。尽管如此，如果没有合适的模型，就很难解决为什么结果会随着社区复杂性的增加而变化的确切原因。

基于模型的方法可以通过多种方式实现，但其核心使用两个步骤（图3）。第一个步骤涉及使用统计模型来量化个体生物的人口统计学表现如何依赖于自然发生的（或实验施加的）邻居丰度和身份的变化。然后，可以使用拟合的模型来量化非传递性竞争的普遍性（76）或高阶项的重要性（59）。第二步涉及使用模型在拟合关系的基础上预测群落动态（图3）。这些预测可以建立在按生物阶段（大小）或年龄构建的人口统计学模型的分析表达式或多物种模拟上。然后，可以通过预测在存在或不存在该机制的情况下竞争的结果来量化某一特定机制对共存的重要性。另一种选择是构建不同机制的动力学模型，然后将这些模型直接拟合到观测到的大量变化中。然而，一些只有微弱统计支持的共存机制可能会强烈影响动力学，因此有必要采用本文所提倡的方法，即先使用模型拟合，再使用投影。

图3 数据驱动的物种动态建模方法

观测或实验数据可以拟合到模型中，然后用于分析相互作用链或高阶相互作用对动力学的影响。年之间的丰度模式（顶部）被转换成人口规模的函数（中间）。对于基于尺寸的模型，所有个体可以被认为是给定区域的圆。物种i (Si)从一年到下一年的大小变化可以建模为在给定半径或邻近区域内其他个体的丰度或集体大小的函数，假设成对或高阶相互作用。类似的模型也可以用于生存和繁殖。然后可以使用拟合的函数来通知基于个体的或整体的社区动态投影模型（下图）。这些模型及其参数可以被操纵以增加或删除特定的共存机制，从而使它们对多样性维持的贡献得以评估。

为了举例说明如何通过拟合模型来量化高阶相互作用的结果（尚无实证研究完成），可以将在纯成对相互作用假设下预测的群落动态与拟合的高阶相互作用也起作用时观察到的动态进行比较。同样，为了理解非传递性竞争如何很好地稳定共存，可以迫使种内的两两相互作用与种间的相互作用相匹配，这样就只剩下非传递性来稳定动态。

尽管需要与经验数据相适应的数学模型，但建立数学模型面临着巨大的挑战——其中最明显的是参数估计和模型过拟合的风险。除了描述内在人口统计学表现的参数外，我们还需要描述种内和种间密度依赖的参数，这些参数可能随大小、阶段或年龄以及空间和时间而变化。如前所述，成对相互作用的数量以系统中物种数量的平方增加，而高阶相互作用的数量增长得更快。理想情况下，为了正确估计这些参数，我们应该观察群落中每个物种在竞争物种的所有密度组合下的人均增长率——本质上是一个n维响应面设计。观测数据集往往达不到这一理想（过度拟合的风险很高），特别是当稳定机制使种群接近某种平衡时。在析因设计中操纵几个竞争对手的密度，并检查竞争对手对目标物种个体的成对和相互作用的实验，可能是拟合自然界高阶相互作用的最有说服力的选择。

在多种竞争网络中共存

需要进一步的理论关注来确定非传递竞争和高阶相互作用如何影响共存，以及竞争网络对物种损失的鲁棒性，这些系统比那些可以参数化的经验系统更大。实现这一目标的进程受到以下事实的阻碍：尽管具有n个竞争者的系统的稳定性（理论的经典焦点；见Box 2）可以评估，如果整个系统不稳定，则不容易评估有多少竞争者可以共存。因此，我们主张将重点从n个物种共存的概率转移到如果我们从一定的n值开始，那么有多少比例的物种会共存。这将使我们能够问，例如，高阶或非传递相互作用如何决定在群落破坏和重新定域后可以共存的物种比例，这是一些生态系统中的常见情况。

模拟不容易实现这样的目标，因为从一个真正多样化的系统中可以衍生出大量的子群落。因此，量化可以共存的物种的比例需要建立新的理论，设计不同的实验方案，并使用生态学的新数学工具。目前，这一共存比例仅在高度理想化的竞争模型中确定，在这种模型中，所有成对的相互作用都会导致排斥，因此只有通过非传递竞争才能实现共存。如果成对的赢家和输家是随机确定的，为了构建所谓的随机竞赛图，从n开始时共存物种的数量可以分析计算。虽然随着n的增加，实现所有物种共存的概率变得越来越小，但平均有n/2个物种可以共存。因此，尽管有相当数量的物种灭绝，一个非常多样化的系统仍然可以存在。

预测物种共存比例的理论框架对于评估网络结构如何影响灭绝级联的程度将特别有用。理论上，如果n个物种稳定共存，而n - 1个物种不稳定共存（由于失去一个主要竞争对手），理想情况下，我们可以预测n - 1个物种中持续存在的比例。此外，这一比例如何取决于竞争网络的结构，包括相互作用链和高阶相互作用的结构，是未来研究的一个重要问题。已经为互惠和多营养网络的研究进行的分析在这里可能具有特别的价值。

注意事项

我们提出的论点是，生态学家缺乏经验数据来评估非传递竞争和高阶相互作用在塑造物种共存中的稳定作用。尽管理论表明，这些类型的相互作用在形成物种共存的过程中起着潜在的关键作用，但我们对适当的经验试验的呼吁不应被视为这些因素在自然界中起重要作用的期望——简单地说，我们不知道。此外，其他类型的证据可以用来限制其潜在的重要性。正如本综述中的几点所指出的，依赖于非传递性或高阶相互作用的共存机制的一个统一特征是，两者都依赖于存在足够数量的物种来运作。然而，大量操纵物种多样性的研究结果表明，当一个群落中聚集的物种数量增加时，新物种进入就变得更加困难了。这一发现可能反映了这样一个事实，即产生这种模式的传统成对生态位机制压倒了共存机制的运作，共存机制只有在更大的竞争对手群体中才会出现。

需要谨慎的另一个原因是，生态学家确实有合理的替代方案，它们完全依赖于成对机制来解释在许多生态系统中看到的非常高的多样性。空间环境异质性是维持物种多样性的强大力量，即使在小得惊人的尺度上也是如此。尽管似乎不太可能在一个多样化的群落中，每个物种都有特定的环境偏好，但只要物种的平均适应度相似，物种之间的适度差异就可以维持共存（Box 1）。自然界中的共存也可能是由成对机制和那些需要两个以上物种的机制之间的相互作用造成的。非传递竞争关系中的空间异质性，或异质互惠或对抗的网络结构，可以极大地有利于区域尺度的共存。此外，在非传递性竞争循环下共存的周期性特性在环境中产生了时间变化，通过这种变化，许多其他物种可以特殊化并最终共存。

展望

在这篇综述中，作者认为共存机制只出现在有两个以上竞争者的系统中，对物种丰富群落的多样性维持起着很大程度上未被探索的控制作用。我们还强调，当研究两个以上的竞争对手时，生态学家必须面对一个生态网络。然而，网络的结构如何影响共存在很大程度上仍然是未知的。证据的稀疏性来自于对许多物种之间的竞争进行经验评估的难处，以及理论与数据紧密耦合所固有的技术困难。尽管存在这些挑战，但仍有令人信服的理由加深我们对这些更复杂的共存机制的理解。有了先进的数据驱动模型和网络分析技术，生态学家至少可以确定一些物种丰富的群落，有多少共存是由只在不同系统中出现的机制造成的。在生态学中，很少有其他问题有如此巨大的潜力，从根本上改变我们对生物多样性的维护和脆弱性的看法。

原文链接

https://www.nature.com/articles/nature22898